My brother was talking about crypto, and got around to claiming that he could design a crypto algorithm that I couldn’t break.
Of course, I have a little bit of experience with cryptography, so I took him up on that bet, under a simple indistinguishability attack. The rules of the game are simple - He, the challenger, provides me the algorithm. I choose two messages, 
Here’s the encryption algorithm he gave me. It’s the classic book cipher - the key is a book, and every character (letter) is replaced by the page number, line number, word number, and letter number of that letter in the book.
As is my usual first try for these things, my two messages were “The quick brown fox jumps over the lazy dog” and “aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa” (the messages have to be equal length - otherwise it’s trivial to distinguish the ciphertext). Also capitalization and spaces are eliminated.
This is the ciphertext:
One thing that we can immediately tell is that the book is at least 784 pages long, since two of the characters are mapped to page 784. The book is also one that’s in our library, which is predominantly paperback scifi books of substantially less than 784 pages. So this dramatically narrows down the set of possible books it could be, so it’s probably feasible for me to go find all books with at least 784 pages and check them.
I won’t do this, however, unless the remaining analysis proves inconclusive.
The plan is to look at the letter number (within the word). In English, the first letter of a word is commonly a consonant, in this sentence alone 21 words started with a consonant and 11 with a vowel (including “a”, not including parenthesized expressions). That’s 2/3rds consonants.
But not all words appear equally often in English (obviously). The word “with” appears much more often than the word “arbitrarily”.
Word frequency lists are a thing that exist, unfortunately the first page on Google appears to be a company that’s selling data gathered from Wikipedia’s article database for hundreds of dollars per seat. I generated this list for another project, so if you want a list of English words ranked by occurrence frequency, use wordcount-tail (the 20,000 most common words in the March 2016 enwiki dump).
Let’s step back for a moment and make an assumption about how the words and letters were picked. Let’s assume that they were picked randomly - that is, my brother tabulated all of the locations of each letter in the book, and then whenever he needed to encrypt a character he chose one of the possibilities at random.
Note that this is not the same as choosing a word at random (out of all of the words containing the letter in question), and then choosing a random letter within that word. Let’s say the book contains 100 words. 99 of the words have exactly 1 “s” as the first letter, and the remaining word is “mississippi”. If you choose a random word, then choose an “s” from the word at random, there is a 99% chance that the “s” will be the first letter of the word (when the chosen word is not “mississippi”). However, if you choose a random letter, there is only a 96% chance that the “s” will be the first letter of the word (when the chosen “s” is not in “mississippi”).
So we’re assuming the former (in a truly formal setting, this would be specified in the algorithm definition, but ‘tis not so). In order to decipher the puzzle, we want to ask: In this model of the world, what are the most likely distributions of letter positions for each message, “The quick brown fox….” and “aaaaa….”? Once we know the most likely distribution for each message, we simply see which distribution looks closer to the actual distribution for the ciphertext, and we guess that is the encrypted message.
For reference, here is the actual observed distribution histogram:
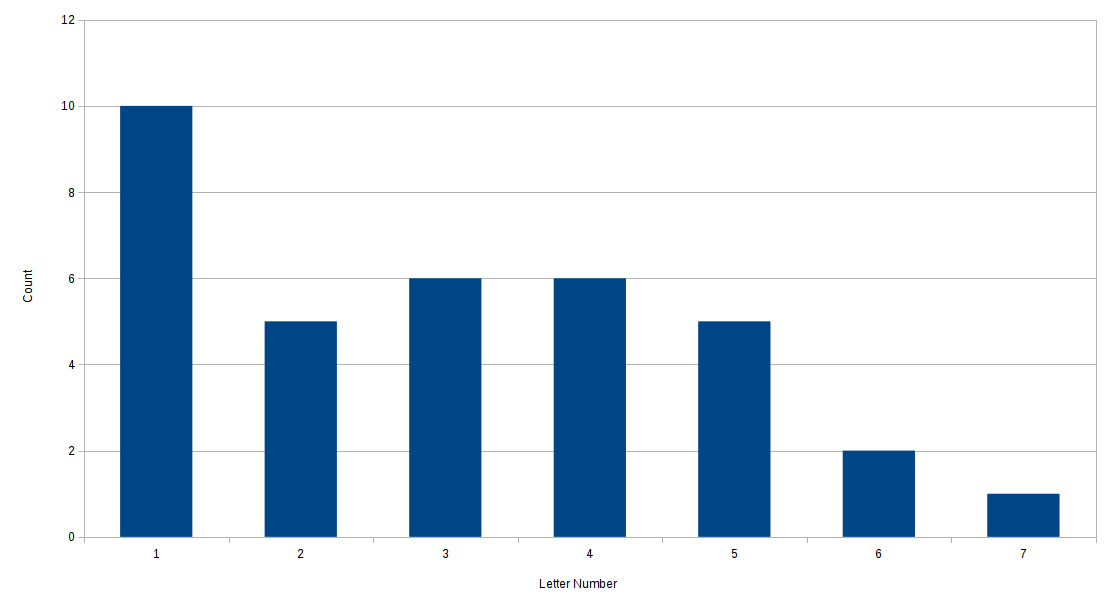
Here we see that a whopping ten letters are the first letter of their respective word (the leftmost bar, over “1”). This drops sharply to only 5 being the second letter (the second bar). Only one letter mapped to the seventh letter of the word.
Now we need to figure out what the histograms look like for “The quick brown fox…” and “aaaaa…” One trivial way to do this would be to generate a large text from our wordlist, and then simply choose letters at random from it. This is not the most efficient way to do that, though.
Let’s say that we have a book with 698,902,632 words in it (the total number of words represented by wordcount-tail.txt). Doing a little math, we find that there are 4,422,856,697 total letters represented. So, if the letter “a” appears (say) 1 billion times in the corpus overall, and 500 million times as the first letter, then if we pick an “a” at random there will be a 50% chance that it’s the first letter of the word it’s in.
I wrote a short script to tabulate the occurrences of each letter in each position, weighted by word frequency:
words = [(word, int(count)) for word,count in [line.strip(" \r\n").split(" ") for line in open("wordcount-tail.txt").readlines()]]
totalBookSize = sum([count for _,count in words])
print("%s words are represented"%totalBookSize)
totalLetters = sum([len(word)*count for word,count in words])
print("%s total letters"%totalLetters)
frequencies = {}
for letter in "abcdefghijklmnopqrstuvwxyz":
frequencies[letter] = [0]*7
for word,count in words:
for i,letter in enumerate(word):
if i < 7 and letter in frequencies:
# We only care about 0-6
frequencies[letter][i] += count
for letter in "abcdefghijklmnopqrstuvwxyz":
print(letter+","+",".join([str(s) for s in frequencies[letter]]))
As an example, here’s the resulting histogram for the letter “a”:
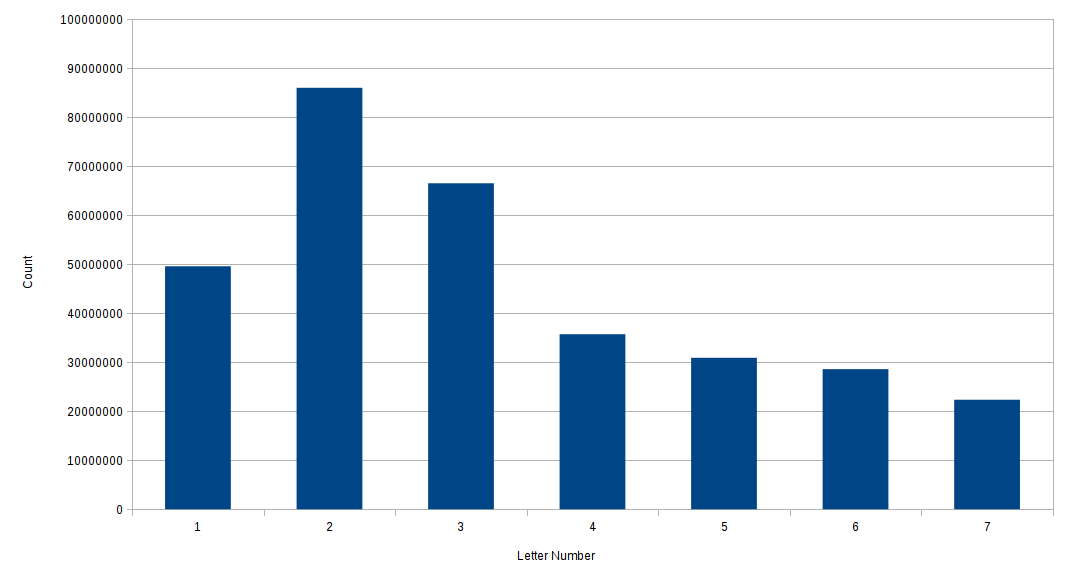
This is much different from the previous graph, which had a large number at position 1, and then a shallow hill around positions 3 and 4. This has relatively few “a”s at position 1, and then strictly decreasing after position 2 (the dataset doesn’t contain the word “a”, so that could be throwing me off). This histogram for “a” is what we would expect in our world model if the ciphertext encrypted “aaaaa…” - Since this is so different in shape from the observed histogram, I want to tentatively say that the ciphertext is “The quick brown fox…” encrypted.
However, just to be sure, let’s look at the histogram for the phrase “The quick brown fox…”. To compute the histogram for the whole phrase, we multiply each row by how many times the given letter appears, and then add up all of the rows. If we do this, we get this histogram:
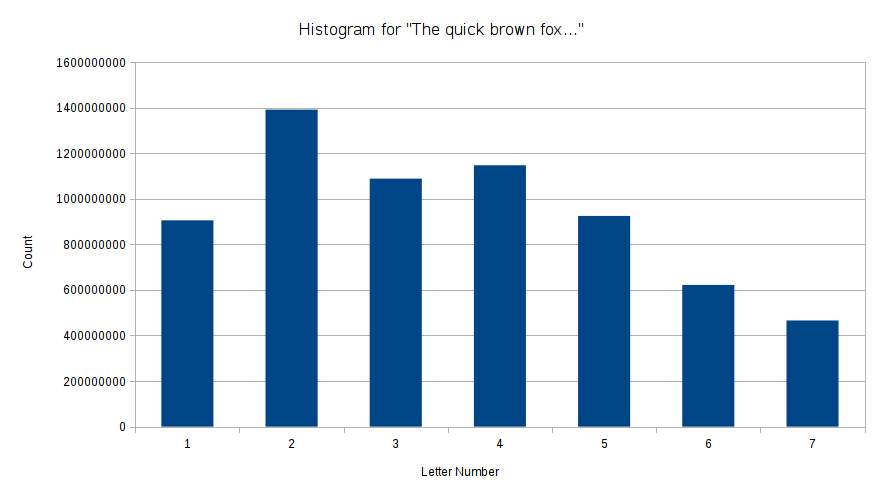
Both of the simulated histograms strongly disagree with the observed ciphertext for letter numbers 1 and 2. The observed ciphertext has a lot of letters from the first letter of the word, and comparatively few from the second letter, whereas both simulated ciphertexts have the opposite.
One possible (psychological) explanation for this is that, when scanning a page for a letter, it is easiest to see the first letter of the word, because the first letter is next to a space. If you’re looking for an “a” in the middle of a page of text, it’s easier to find a standalone word “a” or the first letter of “affordable” or “argue” than it is to see if in the middle of the word “disagree”. The lower count of second letters could be because humans are terrible at choosing randomly (this has been established many, many times), and perhaps chose the second letter disproportionately less often to try to appear random.
Another explanation could be that my wordlist is faulty. It is known that it doesn’t have the word “a” (or, apparently, any two-or three-letter word such as “if” or “the”), so if the encrypted text is really “aaaaa…” then that could cause the model to be dangerously skewed.
However, for the 3rd, 4th, 5th, 6th, and 7th letter numbers, the “quick brown fox” histogram agrees much more closely with the observed than the “aaaaa” histogram. The observed and the “quick brown fox” both feature places 3 and 4 agreeing closely with each other, and 5 through 7 decreasing from there, whereas “aaaaa” has place 3 substantially more common than 4.
For this reason, I guessed that “The quick brown fox jumps over the lazy dog” was the encrypted text.
I guessed right.
So there, statistical analysis can work even with small sample sizes.
For reference, here’s my spreadsheet (in LibreOffice Spreadsheet format) containing all three graphs and numbers:
